Welcome to Cikgu Azlin's blog: Nombor Kompleks

Nombor kompleks ialah gabungan nombor nyata dan nombor khayalan. Nombor kompleks mempunyai bentuk:

a + bi \,

di mana a dan b ialah nombor nyata, dan i ialah unit khayalan.

i

bersamaan dengan

\sqrt{-1}

a

dipanggil bahagian nyata nombor itu, dan

b

dipanggil bahagian khayalan. Nombor nyata boleh disebut sebagai nombor kompleks dengan

b = 0

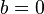, manakala nombor khayalan pula boleh disebut sebagai nombor kompleks dengan

a = 0

.
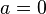Contohnya,

3 + 2i

ialah sebuah nombor kompleks dengan bahagian nyata 3 dan bahagian khayalan 2. Katakan

z = a + bi

, bahagian nyatanya ditulis

\mathrm{Re}(z)

atau

\mathfrak{R}(z)

, manakala bahagian khayalannya ditulis

\mathrm{Im}(z)

atau

\mathfrak{I}(z)

.
Nombor kompleks boleh dicampur, ditolak, didarab dan dibahagi seperti nombor nyata, tetapi dengan sifat lain. Contohnya, nombor nyata sendiri tidak boleh memberi jawapan untuk semua persamaan polinomial, manakala nombor khayalan boleh.
Dalam beberapa bidang (terutamanya kejuruteraan elektrik) di mana i ialah simbol untuk arus elektrik, unit khayalan ditulis j.

Kesamaan

Dua nombor kompleks adalah sama jika dan hanya jika bahagian-bahagian nyatanya sama dan bahagian-bahagian khayalannya sama. Dalam kata lain, jika dua nombor komples ditulis sebagai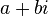

a + bi

dan

c + di

dengan

a

b

c

, dan

d

adalah nyata, maka kedua-dua nombor itu adalah sama jika dan hanya jika

a = c

dan

b = d

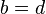Operasi-operasi

Nombor kompleks boleh dicampur, ditolak, didarab, dan dibahagi dengan mengenakan hukum-hukum kalis sekutuan, kalis tukar tertib, dan kalis agihan, serta persamaan

i^2 = -1

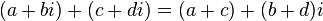
Campur: $\,(a + bi) + (c + di) = (a + c) + (b + d)i$

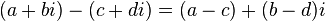
Tolak: $\,(a + bi) - (c + di) = (a - c) + (b - d)i$

Darab: $\,(a + bi) (c + di) = ac + bci + adi + bd i^2 = (ac - bd) + (bc + ad)i$

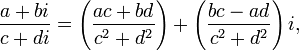
Bahagi: $\,\frac{a + bi}{c + di} = \left({ac + bd \over c^2 + d^2}\right) + \left( {bc - ad \over c^2 + d^2} \right)i,$; di mana $c$ dan $d$ bukan sifar. Ini diperoleh dengan mendarab pengangka dan penyebut dengan konjugat penyebut $c + di$ , iaitu $(c - di)$ .